In this presentation slides we go through various (basic) implementations of SPMV and SPMM on GPU.

A Survey of Sparse Matrix Multiplication on GPUs (CUDA)

Xiang Li

8/18/2022

Revisit – What is GPU & Why HPC on GPUs

GPU Preliminary

Features of GPU:

• MANY core processors
  • performance (throughput) relies on large-scale multithreading
  • up to 80 Streaming Multiprocessors(SMs), each with 100+ ALUs.
• Codes (functions) running on GPU separately called kernels
  • SIMT(Single Instruction Multiple Threads) fashion running scheme
  • 32 threads as an execution unit, called a warp

Comparing with CPU

• With Multi-CPUs
  • Thousands of cores cooperating on a task.
• With CPU multicores
  • The most similar. Cores have both shared resources (memory) and private registers.
  • L1 and L2 cache available. L1 is can be manually manipulated on GPU.
• With SIMD instructions

GPU Preliminary - General steps for a GPU Program

1. Allocate memory on CPU/GPU
2. Prepare data on / transfer data to GPU
3. Computation on GPU
4. Data copied back to CPU
5. Finish up outputs on CPU

GPU Preliminary - Memory manipulation

• Allocate memory on GPU
  • Define stack variables as usual
  • Allocate heap variables via cudaMalloc(ptr, size) v.s. malloc(ptr, size)
• Copy data to/from GPU
  • cudaMemcpy(target, source, size, direction)
  • cudaMemcpyAsync - a nonblocking variant
• Do not use host memory addresses in GPU codes!

GPU Preliminary - How to declare a kernel

• You must define GPU codes via functions.

__global__ void kernel_func(int arg1) {}

• __global__ runs on GPU, called from CPU/GPU
  • Only void return is allowed
• __device__ runs on GPU, called from GPU
• __host__ runs on CPU, called from CPU (implicitly added for functions without idenifier)

GPU Preliminary - How to run a kernel

• You must run GPU codes via function calls (from CPU).

kernel_func<<<grid_shape, block_shape>>>(arg1);

• To run a GPU kernels, call a __global__ function with an extra grid and an extra block parameters.
• Grid and block provides information for GPU of how thousands of threads shall be organized.
• Both grid and block can be 1D, 2D or 3D.

Logical thread model: Grids & Blocks

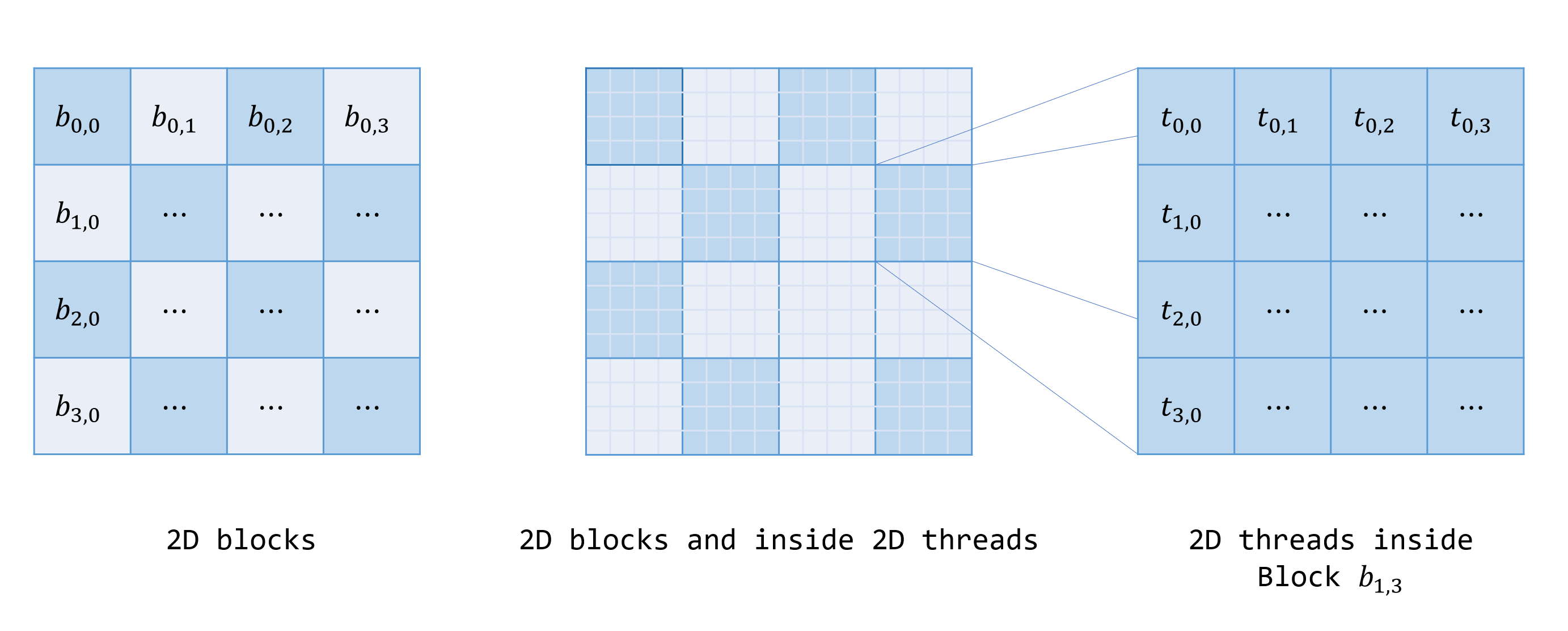Logical Thread Model

• By launching a kernel, all available threads are spreaded in a grid.
• Inside each point is a team (of threads) working on the coming codes concurrently.
  • The team is called a (thread) block, which may also be organized as 1D, 2D or 3D.
• Each team of threads are further divided into sub-teams, called warps, taking turns executing codes.
• Usual warp size is 32(CUDA). These 32 threads execute code simultaneously. This fashion is called SIMT execution.

Turing TU104 Chip Diagram

Physically (Tesla T4):

• 1 GPU = 40 SMs + 16Gb Mem

• Global memory <-> L2 Cache <-> SM

• For computation:
  • 1 GPU = several SM(Streaming Multiprocessors) + Global Memory + Global Scheduler.
  • Global Scheduler schedule incoming blocks to avaiable SMs.
  • 1 SM = Execution Units(ALU,FP32,FP64,Tensor) + Shared Memory (on local chips) + Registers + SM Scheduler.
  • SM Scheduler find and launch eligible warps(32 threads) for the next GPU cycle. Warps become eligible after they fulfill their data dependency.
• For memory/registers:
  • Global memory <-> L2 Cache <-> L1/TEX Cache <-> Execution Units
  • Shared memory <-> Execution Units
  • Registers <-> Execution Units
  • Without cache, global memory is very slow.
  • Shared memory is on the chip hence fast, but usually with limited size (~64KB).
  • A Register file (~256KB) is on the chip and fast as well.

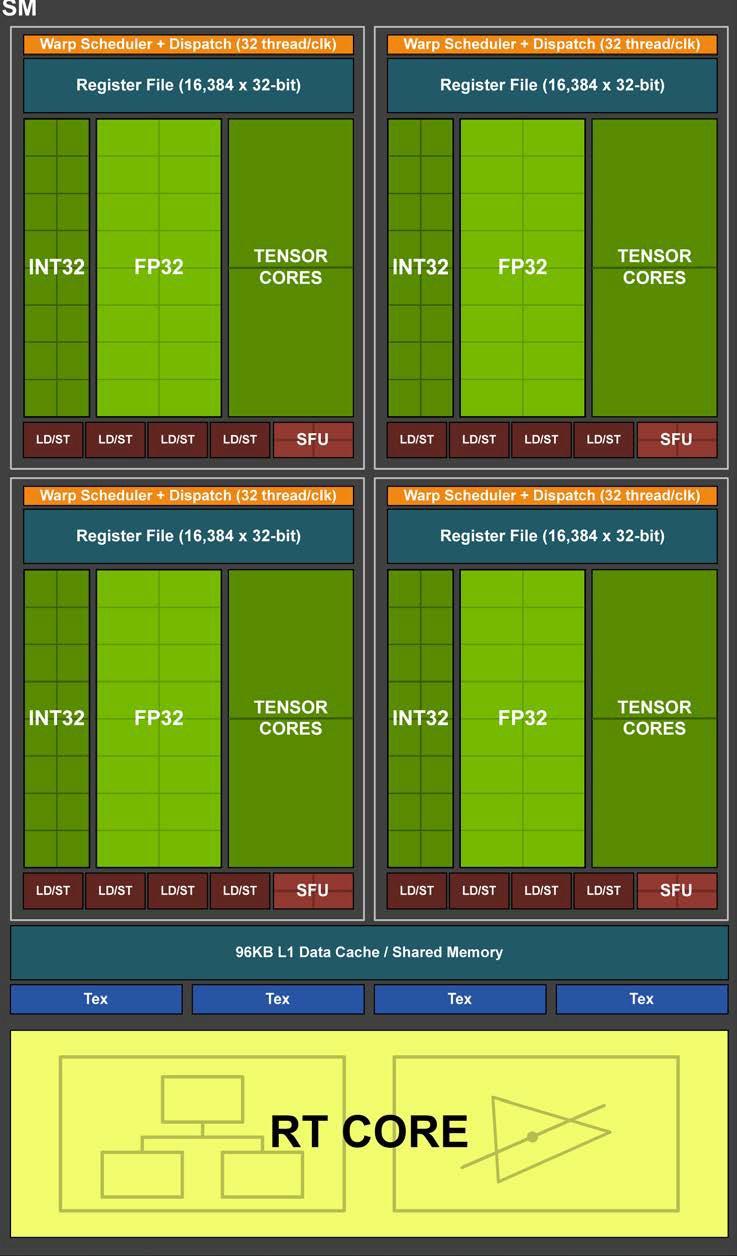Turing TU104 SM

• 1 SM = 64 CUDA Cores + 96Kb SharedMem/L1 Cache + 256KB register
• L2 Cache <-> SharedMem/L1 Cache/Register <-> Execution

Keys to understanding GPU execution logic:

• Block is the parallelization unit.
  • Comprises several sub-teams called warps
  • Within warp threads execute simulatenously
• The block owns a whole shared memory chip and a whole register file.
  • Resource of a block is shared across its warps
• Each thread can use (private) registers as long as not exceeding the total available registers.
  • If exhausted, excessive register values go to global memory

General Ideas on Improving Performance with GPU

• Full utilization of global memory bandwidth of the GPU hardware
  • Make coalesced access pattern to data
  • Profiling metrics:
    • # global load transactions (in every 32B)
    • # global load throughput (in GB/s)

• Full utilization of computation power
  • Adequate size of blocks
    • Large -> Shared memory and registers diluted
    • Small -> Too few eligible warps to launch
  • Minimize thread divergence within a warp
  • Maintain high occupancy

Note: A thread can issue multiple reads (on separate instructions in the instruction stream). Multiple reads from a single thread can be in flight. A read request by itself does not stall the thread. Only when the results of that read are required for a future operation will it stall (if the read data is not available.) The compiler is aware of this and will attempt to schedule reads before the data are actually required. In such scenarios, multiple reads (from a single thread or warp) can be in flight. See ref.

Parallelizing SpMV on GPUs

• There are more than sixty specialized SpMV algorithms and sparse matrix formats (2017)
• We introduce some basic methods from Nvidia team official

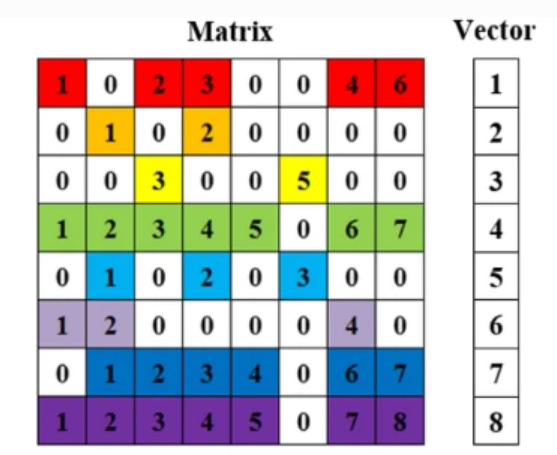SpMV

Sparse Matrix Representation for SpMV

• DIA format for sparse matrix
• ELL format for sparse matrix
• COO format for sparse matrix
• CSR format for sparse matrix
• and many others (HYB, PKT, DCSR, …)

DIA Kernel

• $A$ is represented by offset and data

1 row = globalThreadIdx
2 if row < num_rows:
3   dot = 0
4
5   for n in range(0, cols_per_row):
6     col = row + offset[n]
7     val = data[num_rows * n + row]
8
9     if 0 <= col < num_cols:
10      dot += val * x[col]
11
12  y[row] += dot

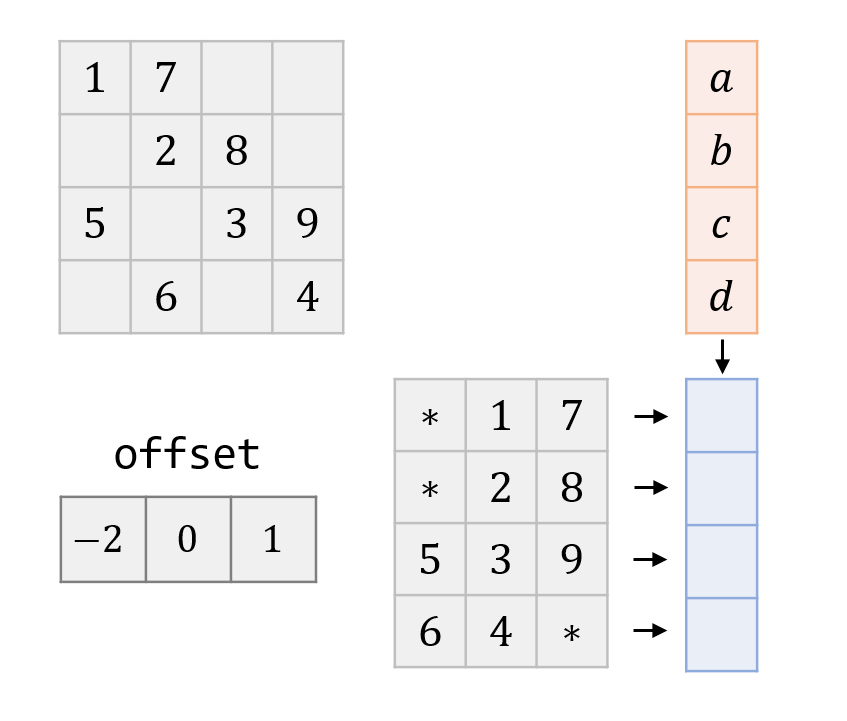DIA SpMV Workflow

• One of the most straight forward: 1 thread / row
• Memory access is contiguous (if col major)
• Padding for completely aligned access of $A$
• Can access offset once per block (pre-load to sharedMem)

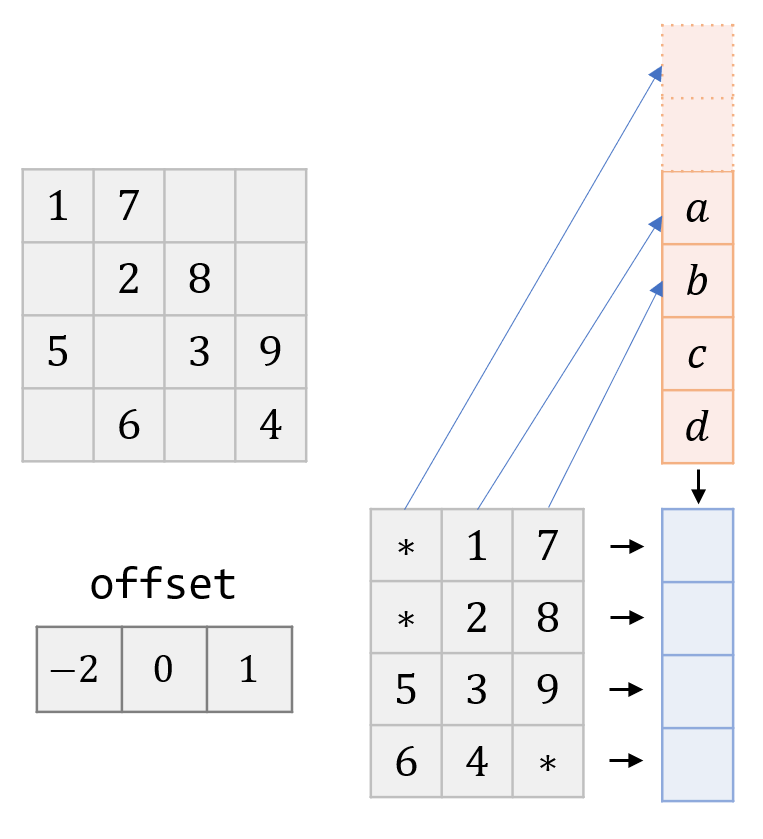DIA SpMV Workflow - Step 1

• Bad performance if pattern unfit for DIA
• Limited number of threads: no more than the number of nonzero diagonals

ELL Kernel

• Very similar to DIA
• 1 thread / row
• Explicit indices, worse performance
• Padding for complete aligned access of $A$
• Not necessarily aligned access of $x$

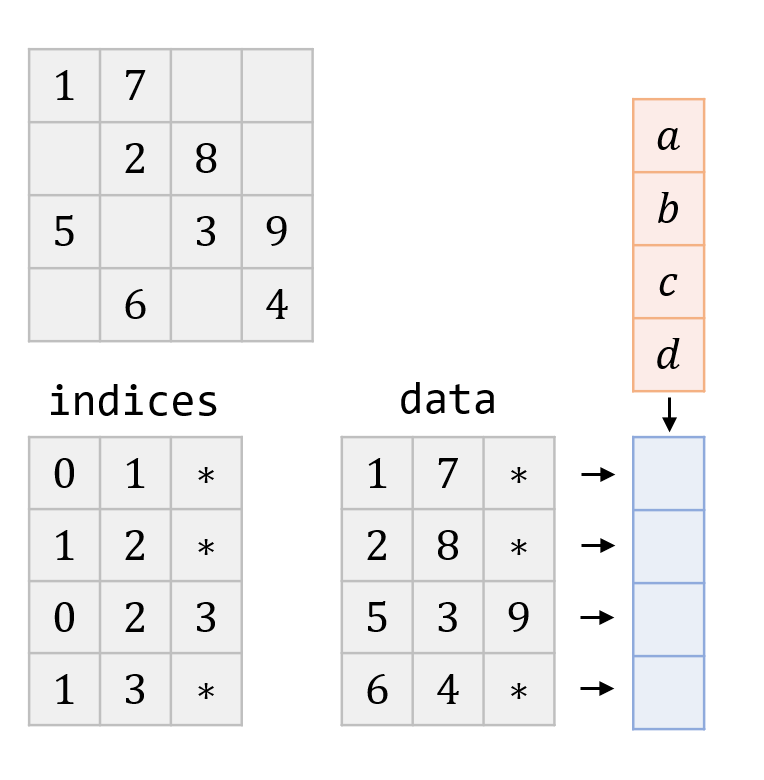ELL SpMV Workflow

1 row = globalThreadIdx
2 if row < num_rows:
3   dot_sum = 0
4
5   for n in range(0, cols_per_row):
6     col = indices[num_rows * n + row]
7     val = data[num_rows * n + row]
8
9     if val != 0:
10      dot += val * x[col]
11
12  y[row] += dot

CSR Kernel (Scalar)

• Straightforward way, 1 thread / row
• Bad access pattern of data (and indicies)
• Thread divergence

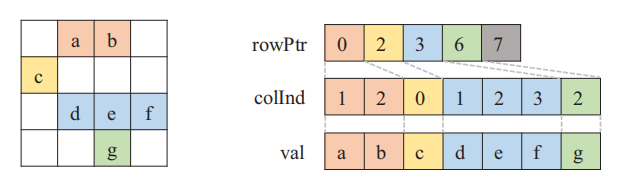CSR Format

Access:      a b c d e f g
----------------------------
Iteration 0: a   c d     g
Iteration 1:   b     e
Iteration 2:           f

CSR Kernel (Vector)

• 1 warp / row
• Resemble vector strip pattern of dot product
• Better parallelization: less in-warp divergence & continuous memory access
• Waste of threads if row nnz < 32

Access: a b | c | d e f | g
----------------------------
Warp 0: a b
Warp 1: c
Warp 2: d e f
Warp 3: g
(Simultaneously)

warp_id = globalThreadIdx // 32
lid = globalThreadIdx % 32  # lane_id
tid = threadIdx

row = warp_id

# on shared memory: vals[]
vals[tid] = 0
for j in range(row_st+lid, row_ed, 32):
  vals[tid] += data[j] * x[indices[j]]

  # todo: sum vals[0:32] to vals[0]
  # parallel reduction

  if lane_id == 0:
    y[row] += vals[tid]

CSR SpMV Workflow

Parallel Reduction in Shared Memory

# simple parallel reduction in shared memory
if lid < 16:  vals[tid] += vals[tid+16]
if lid <  8:  vals[tid] += vals[tid+ 8]
if lid <  4:  vals[tid] += vals[tid+ 4]
if lid <  2:  vals[tid] += vals[tid+ 2]
if lid <  1:  vals[tid] += vals[tid+ 1]

Parallel Scan: All-prefix-sums

• Very important and classical problem
  • Application: stream compaction
• An inefficient $\mathcal O(n\log_2n)$ example algorithm:

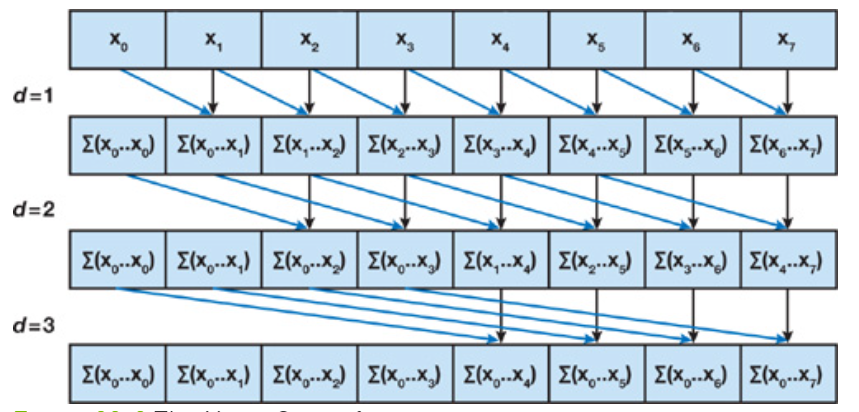Prefix Sum

• Optimizing to $\mathcal O(n)$ is not that easy! (Try if you haven’t read that)

CSR Kernel (Vector) (Cont’d)

• An enhancement for row nnz < 32:
  • Span warp to mulitple rows / Tile rows to one warp
  • Introduce the segment reduction (CSR) problem

Segment starts (CSR):
    0:     0    9   19   25

Values:
    0:     1    5    5    1    2    5    1    1    4    4
   10:     5    3    4    4    4    2    2    4    2    5
   20:     5    1    5    1    4    *    *    *    *    *

Reduced Values:
    0:    25   34   21

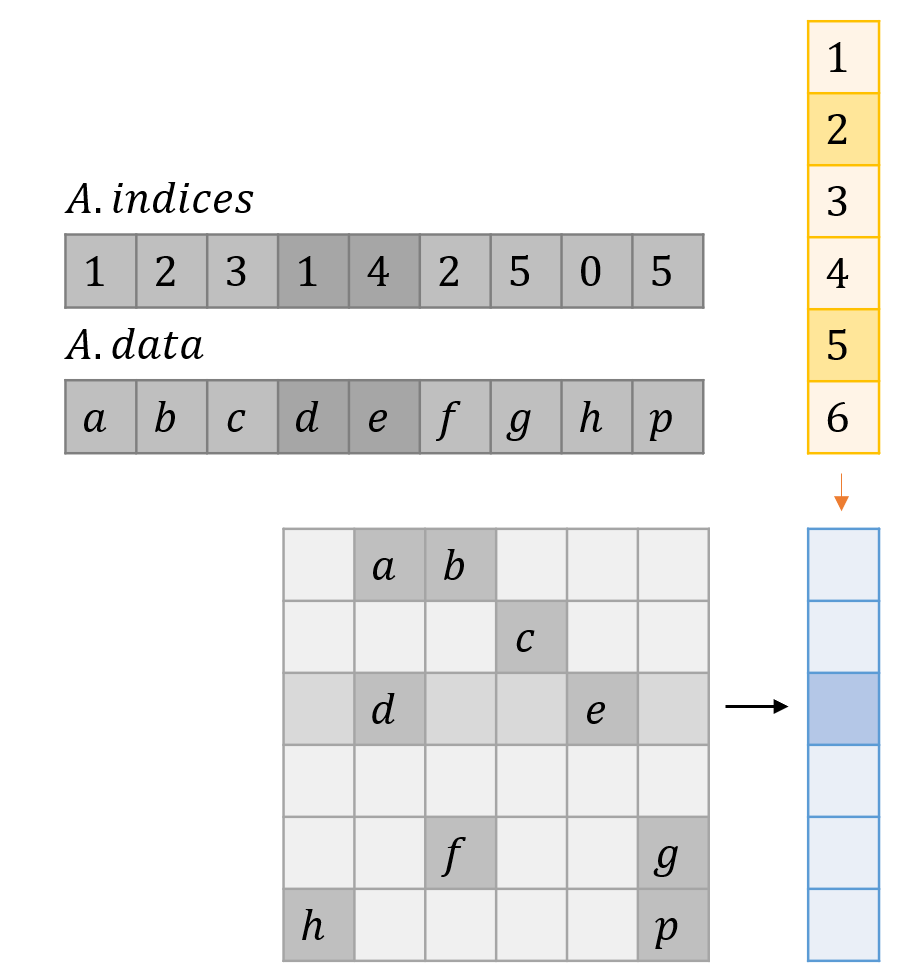
COO Kernel

• Insensitive to sparsity structure
• Segmented row access (multiple rows/warp)
  • Requires segmented reduction (COO)

COO Format

Segmented Reduction (COO)

Keys:
    0:     0    0    0    1    1    1    2    2    2    2
   10:     2    2    2    2    2    2    2    2    2    2
   20:     2    2    2    2    2    2    2    2    2    2
   30:     2    2    2    2    2    3    3    3    3    3

Values:
    0:     2    4    2    4    1    5    3    2    4    4
   10:     2    5    2    2    5    3    3    5    3    3
   20:     2    2    1    4    4    2    1    4    1    3
   30:     1    3    2    4    2    5    1    2    1    5

Reduced keys:
    0:     0    1    2    3
Reduced values:
    0:     8   10   82   14

Segmented Reduction

• A parallel reduction over many irregular–length segments
  • COO–style: reduce by key
  • CSR–style: segment descriptors
• load balance is the key!

Segments         Values                                        Reductions
 0:  5  4                                                       =   9
 1:  5                                                          =   5
 2:  0  0  4  2  5                                              =  11
 3:  1  3  1  5  1  2                                           =  13
 4:  0  3  0  2  3  4  4  3                                     =  19
 5:  2  5  5  0  5  0  3  4  5  1  1  0  5  3  2  3  3          =  47
 6:  3  1  5  4  5                                              =  18

Segmented Reduction (CSR)

Threads    Inputs (* = segment end)       Partials       Carry-out  Carry-in
 0: 5  4* 5* 0  0  4  2  5*              :  9  5 11         =>  0*     0
 1: 1  3  1  5  1  2* 0  3               : 13               =>  3*     0
 2: 0  2  3  4  4  3* 2  5               : 16               =>  7*     3
 3: 5  0  5  0  3  4  5  1               :                  => 23      7
 4: 1  0  5  3  2  3  3* 3               : 17               =>  3*    30
 5: 1  5  4  5* 4  3  3  1               : 15               => 11*     3
 6: 5* 1  4* 5  2  0  0  4               :  5  5            => 11*    11
 7: 4  2  4  4  2  3  2  3               :                  => 24     11
 8: 4  2  0  3* 2  3  5  0               :  9               => 10*    35
 9: 4  0  2  4  2  5  4  0               :                  => 21     10
10: 3  2* 5  4  2  0*                    :  5 11            =>  0*    31

Fixed reductions
 9  5 11 13 19 47 18 16  5 44 36 11

Segmented Reduction (COO) - Inside Warp

# segment reduction in shared memory
if lane >= 1  and rows[tid] == rows[tid-1]:
    vals[tid] += vals[tid-1]
if lane >= 2  and rows[tid] == rows[tid-2]:
    vals[tid] += vals[tid-2]
if lane >= 4  and rows[tid] == rows[tid-4]:
    vals[tid] += vals[tid-4]
if lane >= 8  and rows[tid] == rows[tid-8]:
    vals[tid] += vals[tid-8]
if lane >= 16 and rows[tid] == rows[tid-16]:
    vals[tid] += vals[tid-16]

SpMV Summary

• DIA and ELL are well-suited to structured grids and meshes
  • fast for regular/well-structured matrices
  • suffer from deficiency for highly variant row nnz size
• CSR is popular and general-purpose
  • naive scalar version does not benefit from memory coalescing
  • vector version might lead to inefficiency if row nnz < 32
• COO is robust and complement of previous deficiency
  • worst computational intensity
  • more complex sort and segmented reduction required

Parallelizing SpMM on GPUs

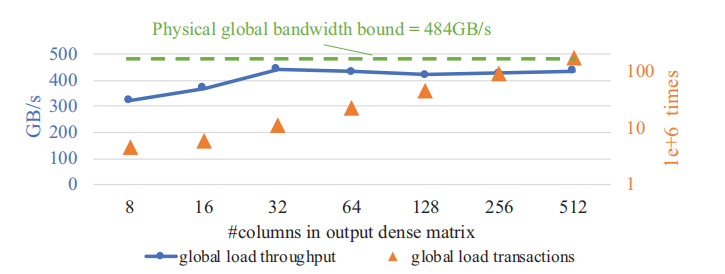Thoughput of SpMM on CUDA

Applications

• pruned NN and GNN
• graph centrality calculations
• all-pairs shortest paths
• iterative solvers with multiple RHS

Existing Software / Packages

• cuSPARSE implementation of SpMM can reach throughput of 450GB/s. (csrmm, csrmm2 in cuSPARSE)
• ELLPACK and its variants
• Customize formats other than CSR for storage

From SpMV to SpMM

• Multiple threads for Mutiple SpMV (CSR scalar)
• Multiple warps for Multiple SpMV (CSR vector)

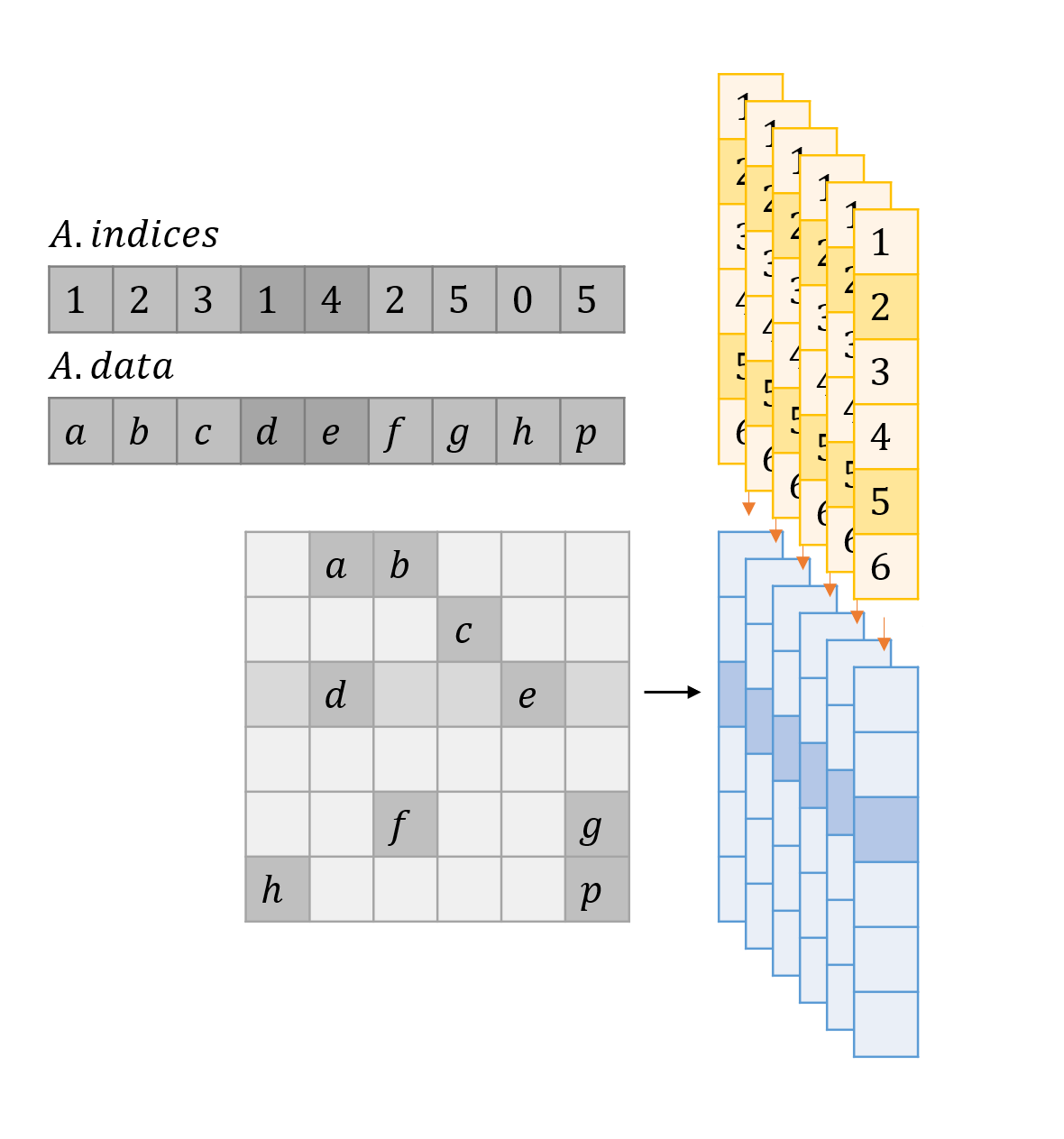From SpMV to SpMM

Original data organization

# Simple implementation of CSR-based SpMM

# All examples of range-like for-loop is exclusive for the last element

# for sparse (CSR) A: A.rowptr[], A.colind[], A.val[],
# for dense        B: B[]
# for dense        C: C[]

1   for i in range(0, M):         # in parallel
2       for j in range(0, N):     # in parallel
3           result = 0
4           # dot product of A[i, :] and B[:, j]
5           for ptr in range(A.rowptr[i], A.rowptr[i+1]): # cannot parallelize!
6               k = A.colind[ptr]                         #
7               result += A.val[ptr] * B[k, j]            # <- reduction must be serial
8         C[i, j] = result

Access pattern for this code

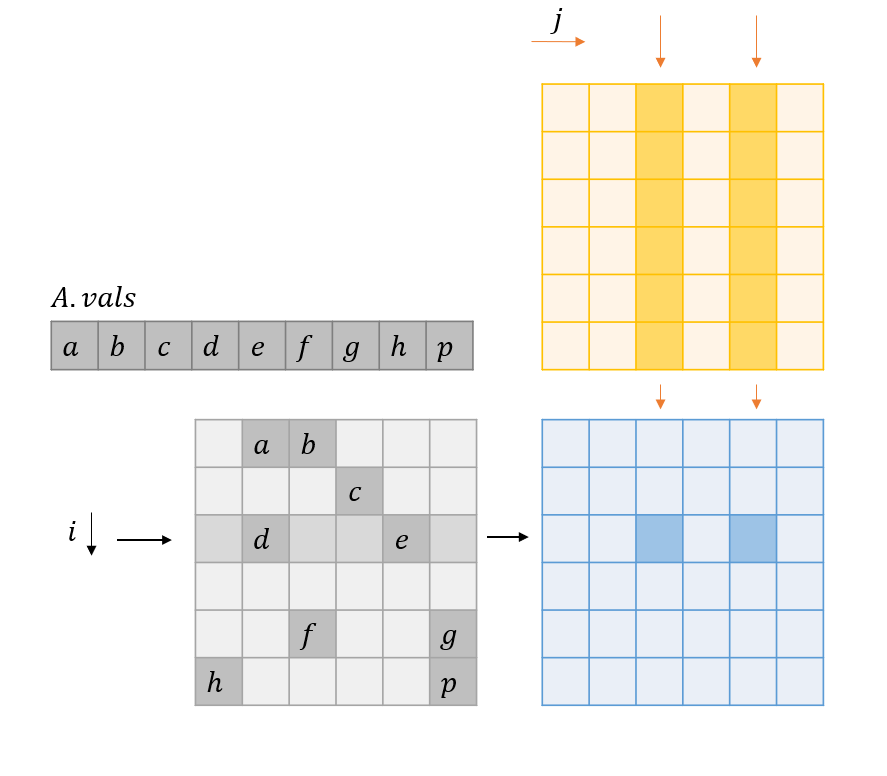SpMM Access Pattern

Observation 1 (Sharing same $A$ rows) Threads within a warp have the same $i$ and contiguous $j$ to parallize the code above.

Observation 2 The sequential execution of the for-loop in line 2 forces threads in the same warp to access the same address.

Coalesced Row Caching (From vector CSR SpMV)

# Improved implementation of CSR-based SpMM (Coalesced Row Caching)
# A.rowptr[], A.colind[], A.val[], B[], C[], block_size (1D grid and 1D block)

# shared memory declared to use: sm_k[block_size], sm_v[block_size]

# Each block handle several rows of A = threads // 32, i.e., each warp handle one row of A
# data in B are partitioned into 32-cols-by-32-cols, and traversed row by row (Row-major stored B prevails)

# This code snippet computes matmul(A[i, 0:32], B[0:32, :])
1   i = block_id * (block_size // 32) + (thread_id) // 32
2   j = lane_id = thread_id % warp_size
3   sm_offset = tid - lane_id  # offset for this warp
4   row_start = A.rowptr[i]  # different warp read different rows!
5   row_end = A.rowptr[i+1]  # they get different row st/ed
6   result = 0
7   for ptr in range(row_start, row_end, warp_size):
8      # load data to shared memory
9      if ptr + lane_id < row_end:
10          sm_k[tid] = A.colind[ptr + lane_id]
11          sm_v[tid] = A.val[ptr + lane_id]
12      __syncwarp()  # ensure data copy inside warp is complete, otherwise race condition
13      for kk in range(0, warp_size):
14          if ptr + kk < row_end:
15              k = sm_k[sm_offset + kk]
16              result += sm_v[sm_offset + kk] * B[k, j]
17  C[i, j] = result

Visualized CRC

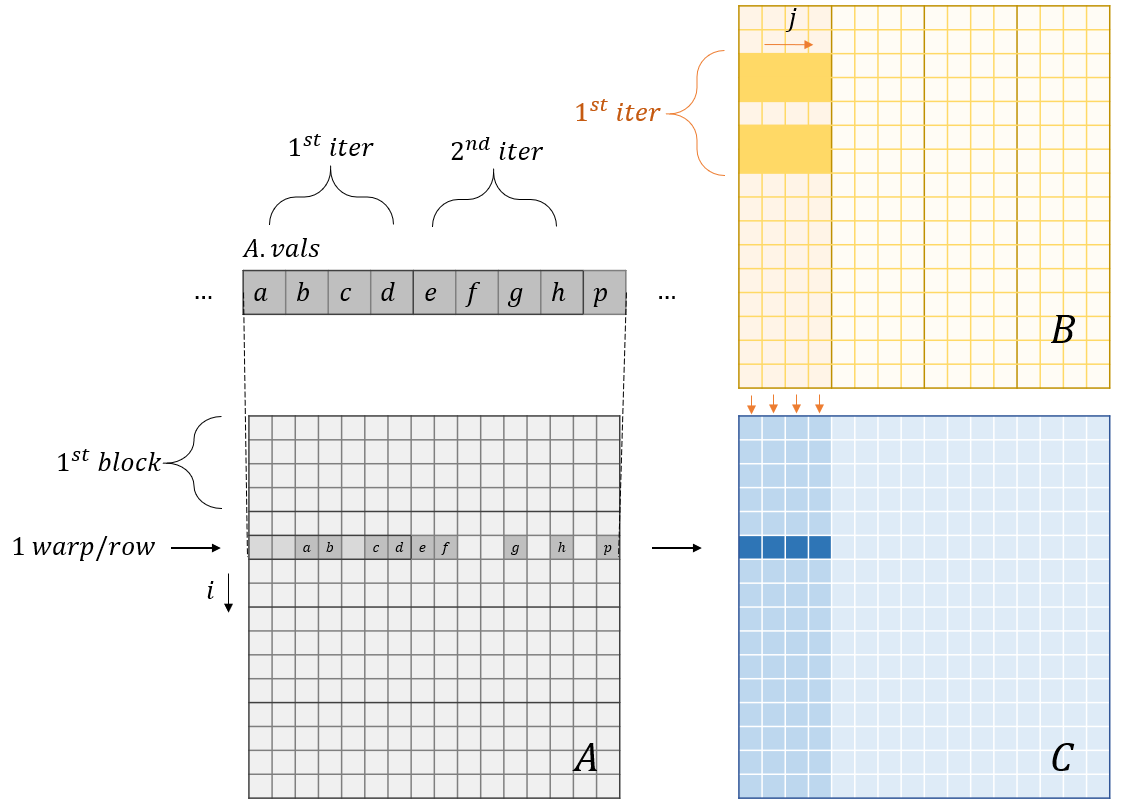Step 1 of CRC

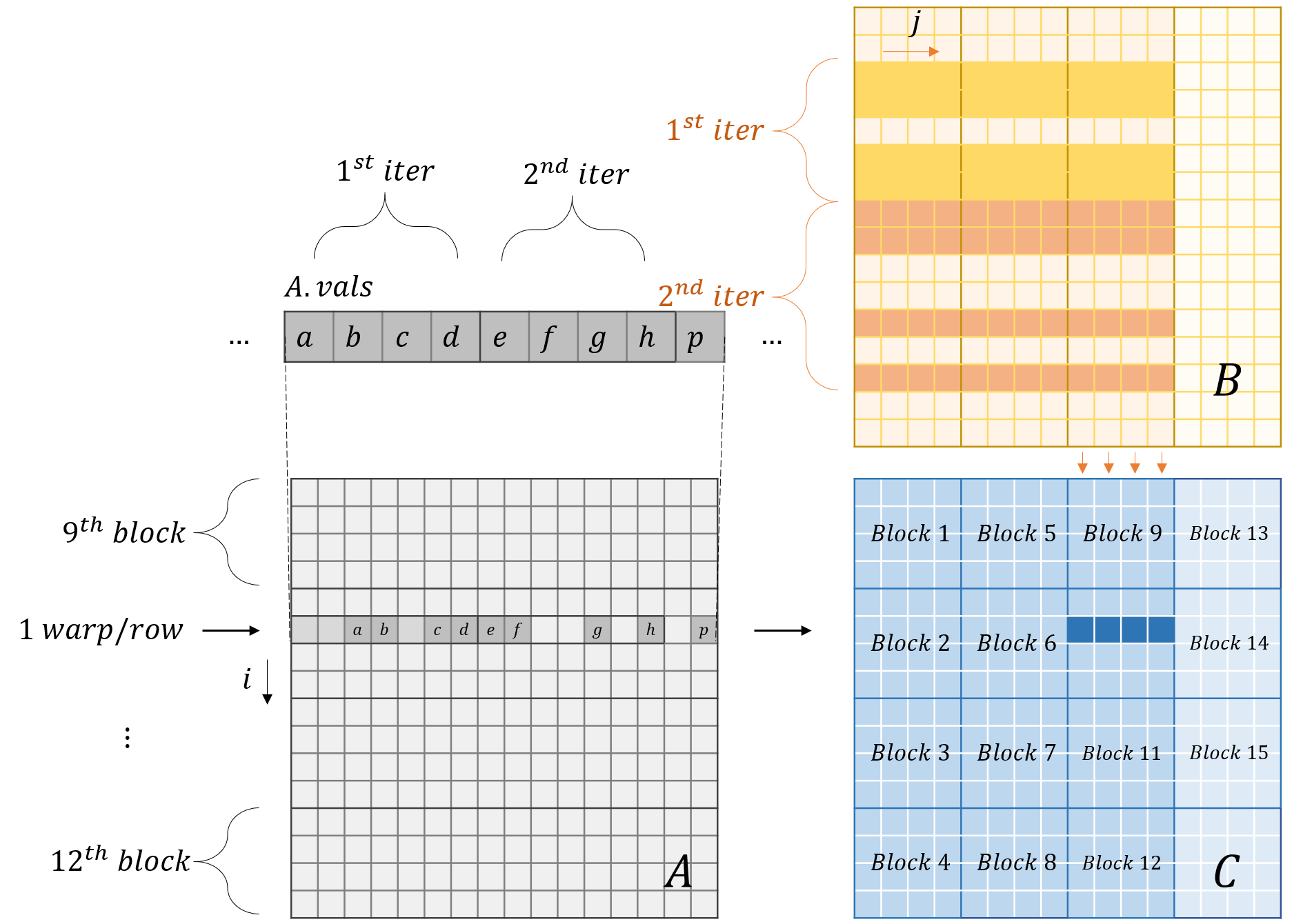Step 2 of CRC

Observation 1 CRC shares loaded sparse matrix via shared memory.

Observation 2 Different warps still perform redundant loading of sparse rows.

Warp Merging

• Reusing shared memory cached $A$
• But reduce the maximum required threads

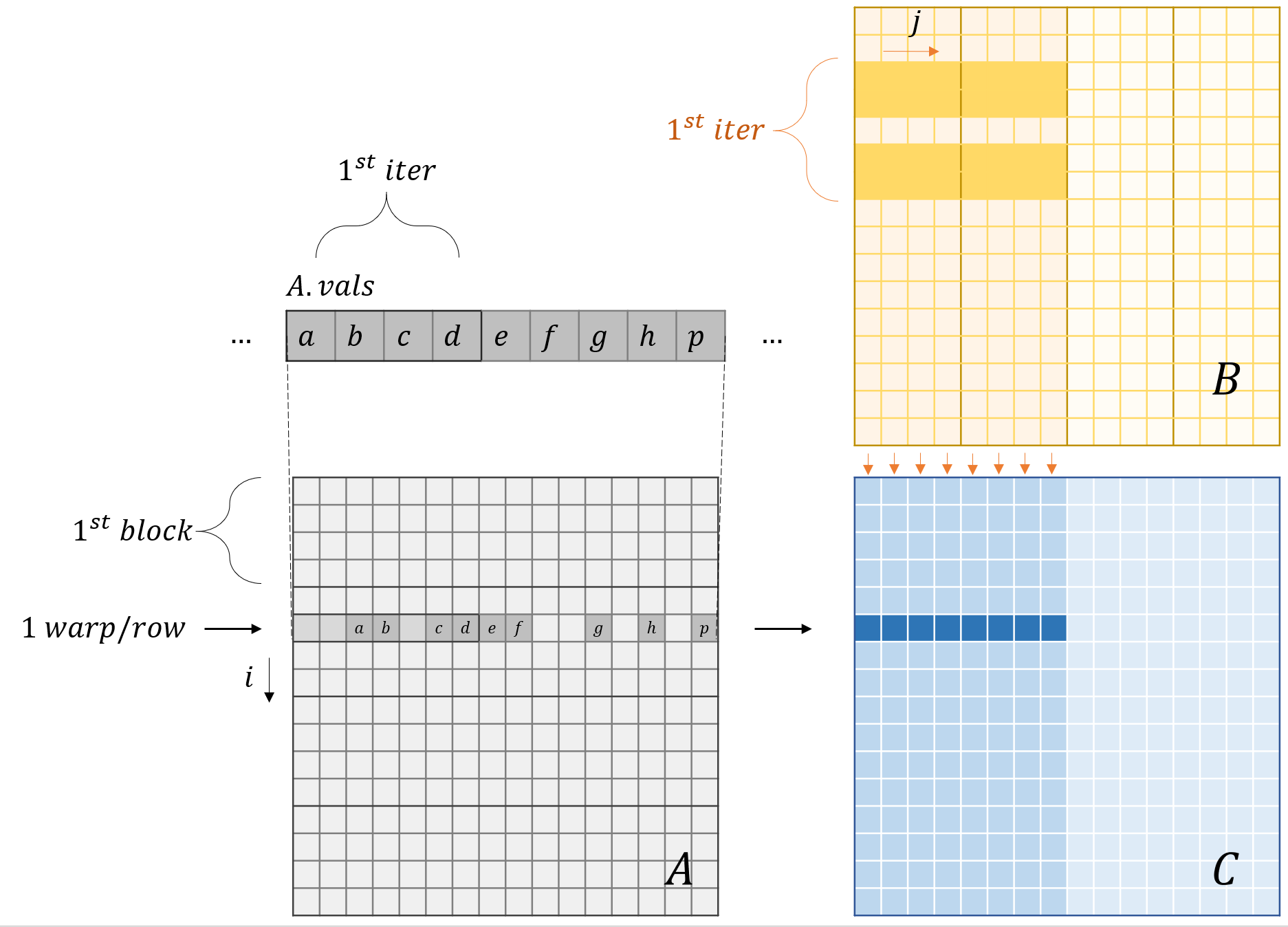Warp Merging

Other important techniques to improve efficiency not covered

• Tiling rows for $A$
• Load balancing permutations (parallel sorting)
• Local dense detection and dense block operations
• Bank conflict resolving
• Cache tuning
• Other sparsity formats

References

1. G. Huang, G. Dai, Y. Wang and H. Yang, “GE-SpMM: General-Purpose Sparse Matrix-Matrix Multiplication on GPUs for Graph Neural Networks,” SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, 2020, pp. 1-12, doi: 10.1109/SC41405.2020.00076.
2. Yang, C., Buluç, A., Owens, J.D. (2018). Design Principles for Sparse Matrix Multiplication on the GPU. In: Aldinucci, M., Padovani, L., Torquati, M. (eds) Euro-Par 2018: Parallel Processing. Euro-Par 2018. Lecture Notes in Computer Science(), vol 11014. Springer, Cham. https://doi.org/10.1007/978-3-319-96983-1_48
3. A. Mehrabi, D. Lee, N. Chatterjee, D. J. Sorin, B. C. Lee and M. O’Connor, “Learning Sparse Matrix Row Permutations for Efficient SpMM on GPU Architectures,” 2021 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), 2021, pp. 48-58, doi: 10.1109/ISPASS51385.2021.00016.
4. Lin, C. Y., Luo, L., & Ceze, L. (2021). Accelerating SpMM Kernel with Cache-First Edge Sampling for Graph Neural Networks. arXiv preprint arXiv:2104.10716.
5. Bell, N., & Garland, M. (2008). Efficient sparse matrix-vector multiplication on CUDA (Vol. 2, No. 5). Nvidia Technical Report NVR-2008-004, Nvidia Corporation.
6. Yan, S., Li, C., Zhang, Y., & Zhou, H. (2014). yaSpMV: Yet another SpMV framework on GPUs. Acm Sigplan Notices, 49(8), 107-118.
7. https://moderngpu.github.io/segreduce.html
8. https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda
9. https://developer.nvidia.com/blog/accelerating-matrix-multiplication-with-block-sparse-format-and-nvidia-tensor-cores/
10. https://developer.nvidia.com/blog/how-access-global-memory-efficiently-cuda-c-kernels/
11. https://developer.nvidia.com/blog/nvidia-turing-architecture-in-depth/